Description

　　平面上的矿区划分成了若干个开发区域。简单地说，你可以将矿区看成一张连通的平面图，平面图划分为了若
干平面块，每个平面块即为一个开发区域，平面块之间的边界必定由若干整点(坐标值为整数的点)和连接这些整点
的线段组成。每个开发区域的矿量与该开发区域的面积有关：具体而言，面积为s的开发区域的矿量为 s^2。现在
有 m 个开采计划。每个开采计划都指定了一个由若干开发区域组成的多边形，一个开采计划的优先度被规定为矿
量的总和÷开发区域的面积和；例如，若某开采计划指定两个开发区域，面积分别为 a和b，则优先度为(a^2+b^2)
/(a+b)。由于平面图是按照划分开发区域边界的点和边给出的，因此每个开采计划也只说明了其指定多边形的边界
，并未详细指明是哪些开发区域（但很明显，只要给出了多边形的边界就可以求出是些开发区域）。你的任务是求
出每个开采计划的优先度。为了避免精度问题，你的答案必须按照分数的格式输出，即求出分子和分母，且必须是
最简形式（分子和分母都为整数，而且都消除了最大公约数；例如，若矿量总和是 1.5，面积和是2，那么分子应
为3，分母应为4；又如，若矿量和是 2，面积和是 4，那么分子应为 1，分母应为 2）。由于某些原因，你必须依
次对每个开采计划求解（即下一个开采计划会按一定格式加密，加密的方式与上一个开采计划的答案有关）。具体
的加密方式见输入格式。

Input

　　第一行三个正整数 n,m,k，分别描述平面图中的点和边，以及开采计划的个数。接下来n行，第 i行(i=1,2,…
,n)有两个整数x_i, y_i,  表示点i的坐标为(x_i, y_i)。接下来m行，第 i行有两个正整数a,b，表示点a和b 之间
有一条边。接下来一行若干个整数，依次描述每个开采计划。每个开采计划的第一个数c指出该开采计划由开发区
域组成的多边形边界上的点的个数为d=(c+P) mod n + 1；接下来d个整数，按逆时针方向描述边界上的每一个点：
设其中第i个数为z_i，则第i个点的编号为(z_i+P) mod n + 1。其中P 是上一个开采计划的答案中分子的值；对于
第 1 个开采计划，P=0。

Output

　　对于每个开采计划，输出一行两个正整数，分别描述分子和分母。

Sample Input

Sample Output

Hint

输入文件给出的9个点和14条边描述的平面图如下所示：

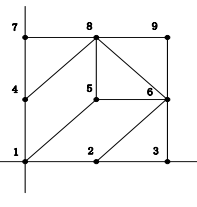
第一个开采计划，输入的第1个值为3，所以该开采计

划对应的多边形有(3+0) mod 8 +1=4个点，将接下的4个数3,0,4,7，分别代入(z_i+0) mod n + 1得到4个点的编号

为4,1,5,8。计算出第一个开采计划的分子为1，分母为1。类似地，可计算出余下开采计划的多边形的点数和点的

编号：第二个开采计划对应的多边形有3个点，编号分别为5, 6, 8。第三个开采计划对应的多边形有6个点，编号

分别为1, 2, 6, 5, 8, 4。第四个开采计划对应的多边形有5个点，编号分别为1, 2, 6, 8, 4。第五个开采计划对

应的多边形有6个点，编号分别为1, 5, 6, 8, 7, 4。

对于100%的数据，n, k ≤ 2×10^5, m ≤ 3n-6, |x_i|, |y

_i| ≤ 3×10^4。所有开采计划的d之和不超过2×10^6。保证任何开采计划都包含至少一个开发区域，且这些开发

区域构成一个连通块。保证所有开发区域的矿量和不超过 2^63-1。保证平面图中没有多余的点和边。保证数据合

法。由于输入数据量较大，建议使用读入优化。

Source